Voici le corrigé du contrôle n°2 (et en cas de besoin, le sujet).
→ À étudier.
[Spé] Divisibilité : utilisation de la récurrence
Voici deux exercices d'entraînement (corrigés), qui peuvent se résoudre en raisonnant par récurrence (le premier exercice peut également se résoudre en utilisant les congruences). Cherchez avant d'étudier le corrigé !
À noter que l'exercice étoilé 1)b) est plus difficile.
[Spé] Corrections (divisibilité)
Voici le corrigé de l'exercice n°9 du polycopié "Arithmétique : autour de la notion de divisibilité".
Également la correction d'une partie de l'exercice n°16 (division euclidienne) du même polycopié, ainsi qu'un exercice supplémentaire corrigé sur le même thème.
→ À étudier en détail
Exercices à chercher pour mercredi 10/10
■ Exercice 1 : déterminer la limite de la suite u définie, pour n > 0, par :
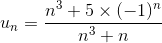
■ Exercice 2 : on rappelle (inégalité démontrée dans le cours) que pour tout réel positif a et tout entier naturel n, on a :
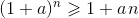
En déduire la limite de la suite u définie pour n > 0, par :
Limites de suites : corrigés de deux exercices supplémentaires
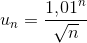
Il est (très) conseillé de chercher les exercices très formateurs suivants :
- n°73 p 55 [ sauf la question c) ]
Indication pour la question 2)a) : en utilisant la méthode "de la quantité conjuguée", prouver tout d'abord que pour tout entier naturel n, on a
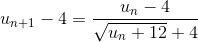
- n°87 p 57
→ Corrigés
Limites et opérations : exercices d'entraînement
Voici des exercices d'entraînement (thème : limites et opérations) avec leurs corrigés (à n'étudier qu'après avoir cherché !).
→ Il est impératif de les chercher.
Correction du contrôle n°1
Voici la correction détaillée du contrôle n°1.
Également la correction de l'exercice V (bonus).
[Spé] Correction du contrôle n°1
Voici la correction du contrôle n°1 de Spécialité (en cas de besoin : le sujet).
→ À étudier.
Récurrence : "soutien" ou approfondissement ?
(I) Voici la correction de l'exercice I.3. du polycopié "Le raisonnement par récurrence" (que nous n'avons pas eu le temps de chercher en classe) → il peut constituer un bon exercice d'entraînement.
(II) Voici les exercices de base sur lesquels nous avons travaillé avec les volontaires en A.P. ce matin (samedi 22/09) :
■ Exercices 14, 13, 24 et 12 pp 19-20.
■ Exercice supplémentaire (particulièrement formateur) :
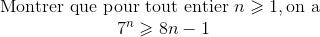
→ Voici la correction détaillée de ces exercices.
(III) Pour ceux qui souhaiteraient se frotter à des exercices plus difficiles, vous pouvez chercher l'exercice n°75 p 26 (voir correction ci-dessus), ou les exercices VI et VII du polycopié "Le raisonnement par récurrence" (corrigés ici et là).
« billets précédents - page 5 de 14 - billets suivants »