oeil de minerve ISSN 2267-9243

L’ouvrage se donne sous la forme de dix-huit « articles » (sans compter la préface), chacun rédigé par un ou deux enseignants et/ou chercheurs.

Le papier est soyeux et de grande qualité, suggérant qu’il s’agit d’un ouvrage se donnant autant à lire qu’à regarder. Ce qui doit aiguillonner avant tout le profane (entendons par là le lecteur non mathématicien), c’est la sensualité de certains modèles (la Surface diagonale de Clebsch par exemple, p. 86) ou leur étrangeté plastique (surface de Kuen, p. 70), qui impulsent l’envie de connaître quelle équation et quelle(s) histoire(s) se dissimule(nt) derrière.

On apprend que l’exigence de modèles mathématiques, soit de figures sculptées, gravés ou construites figurant l’équation de telle surface par exemple, est née avec la géométrie descriptive au XVIII^ème siècle et sous l’impulsion du mathématicien français Gaspar Monge (1746-1818). Il s’agissait, entre autre, de définir des méthodes pour résoudre des problèmes d’ombre entre volumes ou surfaces tridimensionnelles (mais pouvant être représentées dans un espace bidimensionnel - sur une feuille donc). Dans cette optique, on comprend qu’un modèle physique de la figure en question ait pu s’avérer de la plus grande utilité.

 C’est donc conjointement à l’essor d’une nouvelle branche de la géométrie que la nécessité de ces modèles-objets s’est faite sentir.

 Cela a pourtant été contemporain d’autres enjeux, et les plus divers. Par exemple, le rôle pédagogique de ces objets, qui permettaient aux élèves de rendre concrète la fonction ou la figure considérée, et ainsi, en la visualisant mieux, de rendre plus aisée les manipulations géométriques. On retrouve ici l’usage de l’intuition déjà soulevé par Descartes dans ses Regulae ad directionem ingenii : il s’agit bien de mettre la mathématique sous la guise du regard (autant celui du corps que de l’esprit) pour faciliter l’abord des problèmes.

 A cet égard, l’année 1902 est emblématique en France, puisqu’elle marque un tournant dans l’histoire de l’enseignement : on comprend que « les humanités scientifiques sont formatrices de l’esprit au même titre que les humanités littéraires » (p. 51), et la Commission qui doit réviser les programmes, avec à sa tête Gaston Darboux - éminent mathématicien - promeut « l’activité de l’élève et la méthode expérimentale » ; dans les collèges et les lycées, ces solides physiques se multiplient alors.

 Il existait également un enjeu commercial et industriel, lié à l’ingénierie, concernant la fabrication et la collection de ces modèles. On apprend à ce propos que les Allemands ont longtemps surclassé les français, et comment.

 D’autres contributions sont plus orientées vers la « science dure ». L’une d’elle souligne le lien énigmatique qui existe entre les nombres premiers (infinis, mais dont le critère de la distribution n’est toujours pas connu - s’il existe), et les nombres complexes. Ce fil tendu entre deux objets mathématiques apparemment sans lien, c’est au travers de certaines figures que l’article qu’on nous le fait saisir (entre autre, les surfaces de Riemann, qui ressemblant à des espèces de disques spiralés). Ainsi, certains modèles séculaires nous déportent vers les problèmes les plus difficultueux et les plus récents de la mathématique.

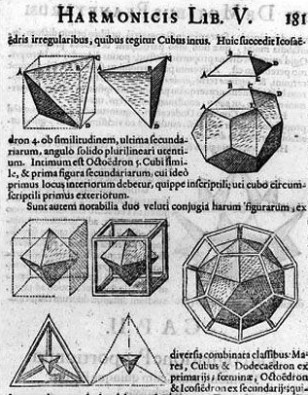
 La collection de l’Institut Henri Poincaré comporte aussi un grand nombre de polyèdres remarquables (article « De Pythagore à Kepler, un voyage polyédrique »), remarquables en ce sens qu’ils sont non seulement réguliers ou semi-réguliers, mais surtout eu égard à leur rôle de premier plan dans l’histoire de la pensée, que ce rôle soit métaphysique, cosmologique ou physique. Dans la contribution en question, il est bien sûr traité des fameux solides de Platon (tétraèdre, hexaèdre ou cube, icosaèdre, dodécaèdre, octaèdre), mais aussi de la liquidation du « rôle idéal des polyèdres réguliers » par Aristote dans l’investigation cosmologique, ainsi que de la découverte par Archimède des polyèdres semi-réguliers (soit « dont les faces sont des polygones réguliers, mais qui peuvent être de nature différente » - une combinaisons de carrés et de triangles équilatéraux par exemple). L’usage des polyèdres courut dans les investigations « scientifiques » a minima jusqu’à Kepler, qui unira « science et métaphysique dans une synthèse grandiose », celle du Mysterium Cosmographicum, où chacune des orbites planétaires sera mis en lien avec l’un des cinq solides de Platon, et où les fameuses trois lois de Kepler sont en germes.

 L’un de moments les plus stimulants de l’ouvrage concerne l’usage de modèles pour rendre sensibles, donc tridimensionnelles, des figures de l’hyperespace (dont la dimension native est strictement supérieure à trois). Autrement dit, il s’agit de visualiser dans « notre » espace un objet qui l’excède par nature. Ainsi, aux cinq polyèdres de Platon correspondent, dans l’hyperespace, les polytopes réguliers, dont certaines des représentations nous sont données dans l’ouvrage (celles de l’hyper cube, de l’hyper tétraèdre et de l’hyper octaèdre).

 Plus intéressant encore, le principe de construction de ces hyper figures nous est visuellement expliqué. De la même manière que pour construire un volume à trois dimensions on opère une translation de surface (un cube n’est que l’espace occupé par deux carrés, dont l’un résulte du déplacement de l’autre), pour construire un hyper cube dans notre espace à trois dimensions, il s’agit aussi de déplacer un cube (à trois dimensions donc) dans ce même espace.

 Un autre article se penche sur la visualisation, via logiciel, des variations d’une même équation (« L’incroyable pouvoir de l’inspiration, de l’intuition et de l’interaction »). Il est phénoménologiquement captivant de donner à voir la traduction formelle (spatiale) d’une modification algébrique. Ainsi, le passage de l’équation x² + y² + z² - 2 = 0 à x² + y² + z² - 0,4 = 0 correspond à la diminution du volume d’une sphère, quand le changement de x² + y² + z² - 2 = 0 en x² + 2y² + z² - 2 = 0 accuse le passage d’une sphère à un ellipsoïde.

 On comprend, dans le premier cas, que l’importance du nombre retranché renseigne négativement sur la taille de la sphère, et dans le second, que le facteur attaché à la deuxième inconnue joue sur la dilatation ou la contraction de la sphère dans la largeur (l’axe des abscisses). Ainsi, peut-on rattacher chaque nombre de l’équation à son rôle « figural ».

 D’autres articles enfin se penchent sur le statut de la collection, qui oscille entre l’héritage patrimonial, la chose utilitaire à vocation scientifique et la nature de quasi œuvre d’art. Ils soulèvent les différentes modalités de conservations des modèles ( a - préventive (qui limite les dégradations), b - curative (qui stabilise les dégradations), c - la restauration comme telle ; cf. « La préservation d’objet scientifiques devenus œuvres d’art »). Il est aussi question de l’histoire particulière qui lie certains modèles de la collection à d’illustres noms de l’art contemporain, Man Ray entre autres, qui les photographia et fit même des séries de tableaux à partir de ses clichés. Avec lui, il est donc question de modèles concrets (puisqu’ils sont l’instanciation de figures mathématiques), mais ressaisit dans un processus artistique abstrait (cf. : « Man Ray à l’Institut Henri Poincaré : des objets mathématiques aux équations shakespeariennes »).

On l’aura compris, il s’agit presque d’un livre d’images, mais protéiforme, exigeant et en lien avec les champs les plus divers, le point d’impulsion initial étant la collection de l’Institut Poincaré. 

BARBEI Julien