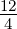l d’eau, c’est à dire 3 l d’eau.
Dans un tableau de proportionnalité, si l’on connaît trois valeurs sur quatre, alors on peut calculer la quatrième.
Cette valeur est appelée la quatrième proportionnelle.
Exemple :
Le volume d’eau, en litres, qui s’écoule d’un robinet est proportionnelle à la durée d’ouverture du robinet, en minutes.
| Durée (en min) | 1 | 4 | 6 |
| Volume d’eau (en l) | ? | 12 | ? |
Donnée de l’énoncé : En 4 minutes, il s’écoule 12 l.
Passage à l’unité : En 1 minutes, il s’écoule 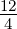l d’eau, c’est à dire 3 l d’eau.
3 est le coefficient de proportionnalité.
En 6 minutes, il s’écoule : 3 l × 6 =18 l d’eau.
Calcul mental : 13 p 90
21 ; 23 ; 24 p 91
Exemple 1 : en faisant la somme de deux colonnes
| Durée (en min) | 4 | 6 | 10 |
| Volume d’eau (en l) | 12 | 18 | ? |
4 min + 6 min = 10 min
12 l + 18 l = 30 l
Donc en 10 min, il s’écoule 30 l d’eau.
Exemple 2 : en multipliant les valeurs d’une colonnes par un même nombre
| Durée (en min) | 6 | 24 |
| Volume d’eau (en l) | 18 | ? |
24 = 6 × 4
Donc en 24 min, il s’écoule 18l × 4 = 72l d’eau.
Exemple
La prime annuelle d’un vendeur est proportionnelle au montant des ventes qu’il a réalisées pendant l’année.
Le directeur du magasin utilise le tableau suivant pour verser les primes à ses vendeurs.
Aidons-le à compléter les cases vides.
| Ventes (en €) | 2000 | 8000 | 18000 | 20000 | 38000 | |
| Primes (en €) | 500 | 1000 | 1125 | 1250 | ||
solutions
| Ventes (en €) | 2000 | 8000 | 16000 | 18000 | 20000 | 38000 |
| Primes (en €) | 125 | 500 | 1000 | 1125 | 1250 | 2375 |
Dans un tableau de proportionnalité composé de deux lignes on peut compléter une colonne :
par somme ou différence de deux autres colonnes;
en multipliant ou en divisant les valeurs d’une autre colonne par un même nombre.
| Durée (en min) | 6 | 24 |
| Volume d’eau (en l) | 18 | ? |
On a calculé précédemment en deux étapes :
24 : 6 = 4
puis 18 × 4 = 72
Il est possible de faire ce calcul en une seule étape :
18 × 24 : 6 = 72
Méthode : on multiplie les deux nombres en diagonale et on divise par le troisième.
Exercices 22 p 91; 27 p 92; 29 et 30 p 92