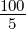 = 20
= 20
Situation 1 :
Anne achète pour 1,50€ de bonbons à la boulangerie. Chaque bonbon coûte 0,15€.
Les deux grandeurs sont "le nombre de bonbons achetés" et "le prix à payer".
prixà payer = nombredebonbonsachetés × 0, 15.
Les deux grandeurs sont donc proportionnelles.
Situation 2 :
A la boulangerie, Eliott lit :
Prix d’une baguette : 0,85€. Pour 3 baguettes achetées, la 4ème est offerte.
Le prix de trois baguettes est le même que le prix de 4 baguettes. Le prix à payer n’est pas proportionnel au nombre de baguettes achetées.
On peut représenter chaque situation dans un tableau en y rassemblant les grandeurs étudiées.
Deux grandeurs sont proportionnelles si les valeurs de l’une s’obtiennent en multipliant les valeurs de l’autre par un même nombre.
Exemple 1 :
| Masse des pommes de terre (kg) | 1 | 5 | 10 |
| Prix des pommes de terre (en €) | 0,8 | 4 | 8 |
Le coefficient de proportionnalité est : ...
Exemple 2 :
| âge (en années) | 5 | 8 | 12 | 24 |
| taille (en cm) | 100 | 136 | 155 | 180 |
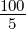 = 20
= 20
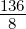 = 17
= 17
Ces deux quotients ne sont pas égaux, donc le tableau n’est pas un tableau de proportionnalité.
Pour reconnaître un tableau de proportionnalité, on peut effectuer chacun des quotients d’un nombre de la seconde ligne du tableau par le nombre correspondant de la première ligne.
Si tous les quotients sont égaux, le tableau est un tableau de proportionnalité; sinon, il ne l’est pas.
Vocabulaire
Dans un tableau de proportionnalité, le quotient commun est appelé le coefficient de proportionnalité.
A l’oral : 5 p 90
16 et 17 p 91