Activité : de la symétrie axiale à la symétrie centrale

Soit M et O deux points du plan.
Le symétrique du point M par la symétrie de centre O est le point M’ tel que O soit le milieu de [MM’].
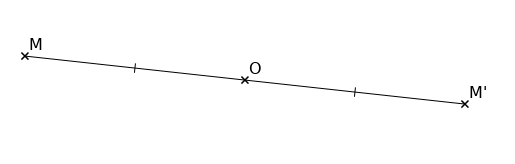
Tracé à la règle graduée, puis tracé au compas.
Méthode pour construire le symétrique d’un point :

Remarques :
Si M’ est symétrique de M par rapport à O, alors M est symétrique de M’ par rapport à O; on dit que M et M’ sont symétriques par la symétrie de centre O.
O est son propre symétrique par la symétrie de centre O.
A l’oral : 11 p 224
On dit que deux figures F et F’ sont symétriques par rapport à un point O lorsque leurs points sont deux à deux symétriques par rapport à O.
O est le centre de symétrie de la figure.
Remarque : les deux figures se superposent en effectuant un demi-tour autour du point O.
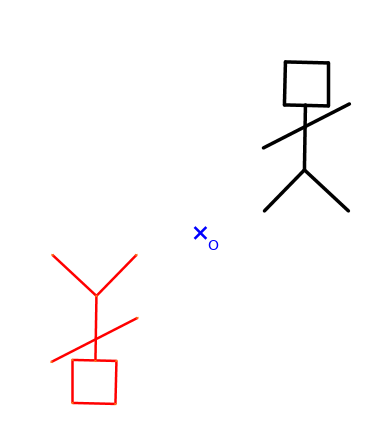

à l’oral : 7 p 224
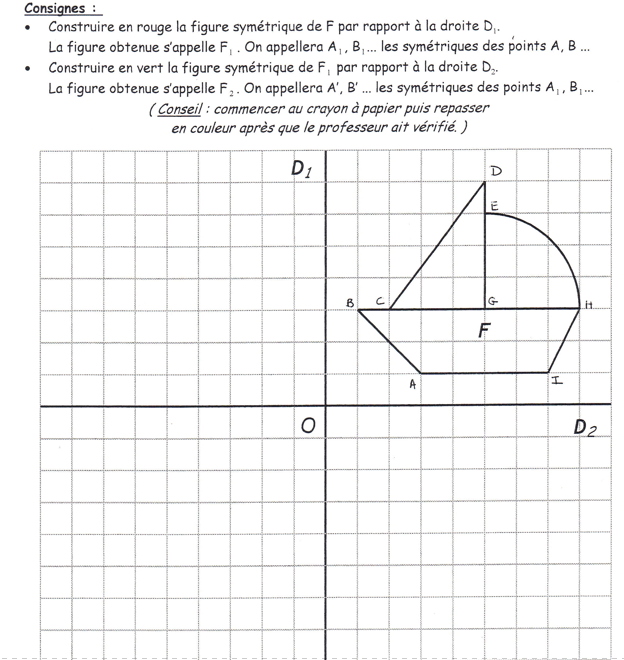
Exercices de construction avec quadrillage (feuille d’exercices)
sans quadrillage : 2 à 5 p 223
à main levée : 27 et 28 p 226
Méthode :
Pour retrouver le centre de symétrie d’une figure :
- on repère deux points symétriques puis on trouve le milieu du segment qu’ils forment.
OU : - on relie deux points symétriques, puis deux autres et on trouve l’intersection de ces deux segments.
à appliquer sur l’illustration Simpson
à l’oral : 12 p 224
Exercices : retrouver le centre de symétrie
DM "Maths et arts"