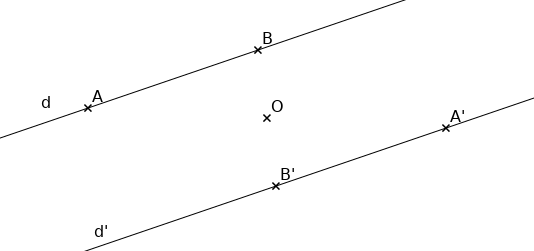
Le symétrique d’une droite par rapport à un point est une droite parallèle.
Exemple : construire le symétrique (d’) de la droite (d) par rapport à O :

Remarque : il suffit de construire le symétrique d’un point.
Exercice : démontrer que les symétriques de deux droites parallèles sont deux droites parallèles (utilisation de la propriété "si deux droites sont symétriques à une même troisième, alors elles sont symétriques entre elles".
Le symétrique d’un segment par rapport à un point est un segment parallèle et de même longueur.
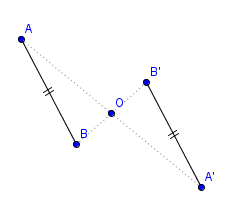
A’B’=AB
et (A’B’) // (AB)
Remarque : le quadrilatère ABA’B’ s’appelle un parallélogramme.
à l’oral : 8 ,9 p 224
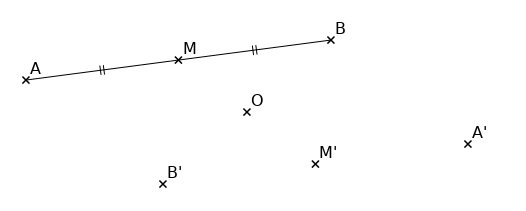
Exercice :
Soit un segment [AB] de milieu M.
a) Construire les points A’, B’, M’ symétriques respectifs de A, B et M par rapport à O.
b) Démontrer que M’ est le milieu de [A’B’].
Résolution :
Comme M est le milieu de [AB], MA=MB.
La symétrie centrale conserve les longueurs, donc M’A’=MA et M’B’=MB.
Donc M’A’=MA=MB=M’B’.
La symétrie centrale conserve :
- les longueurs,
- l’alignement,
- les mesures d’angles,
- les aires.
Une figure et son symétrique par rapport à un point sont donc superposables.
à l’oral : 10 p 224
à l’écrit : 29 à 32 p 226