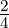 h =
h = 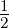 h =
h = 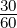 h
h
Exemples :
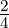 h =
h = 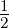 h =
h = 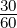 h
h
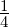 =
= 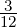 dessin au tableau
dessin au tableau
"si on partage en trois fois plus de parts, les parts sont trois fois plus petites, donc il en faut trois fois plus pour avoir la même quantité."
Un quotient ne change pas lorsque l’on multiplie (ou lorsque l’on divise) son numérateur et son dénominateur par un même nombre non nul.
Exemple :
La proportion d’élèves qui font du latin dans une classe de 30 élèves est de un tiers.
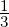 =
= 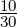
Sur une classe de 30 élèves, il y a 10 élèves qui font du latin.
à l’oral : 13 p 52
à l’écrit : 38, 39, 40 p 54 (en classe)
écrire des fractions égales :
à l’oral : 14 p 52
à l’écrit : 42 à 46 p 54,55
Simplifier une fraction, c’est écrire une fraction qui lui est égale avec un numérateur et un dénominateur entiers plus petits.
Exemples : simplifier 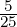 ;
; 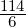
On cherche un diviseur commun au numérateur et au dénominateur. Pour cela, on peut utiliser les critères de divisibilité :
Un nombre est divisible par 2 s’il est pair (c’est dire si son chiffre des unités est 0, 2, 4, 6, ou 8).
Un nombre est divisible par 5 si son chiffre des unités est 0 ou 5
Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3
Un nombre est divisible par 9 si la somme de ses chiffres est divisible par 9
Parmi les nombres suivants : 7410, 184, 279, 1975, 234, indiquer ceux qui sont :
divisibles par 2 : 7410; 184; 234
divisibles par 3 : 7410; 279; 234
divisibles par 5 : 7410; 1975
divisibles par 9 : 279; 234
Simplifier : 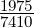 =
= 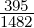 ;
; 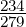 =
= 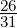
Exercices 50 à 54 p 55