Vocabulaire
Tracer un triangle rectangle ABC, identifier pour un angle le côté adjacent et le côté opposé.
A l’oral : exercices 7 et 8 p 208
Exercices 19 et 20 p 209
Exercice préparatoire :
Reproduire sur votre cahier un angle de même mesure que l’angle α.
Conclusion : le rapporteur ou le compas ne sont pas nécessaires pour reproduire un angle. Il suffit de connaître la pente : ici, il faut prendre 4 unités horizontales, puis 3 unités verticales.
On dit que la pente est de 
, ou de 75% (les pentes sont souvent exprimées en pourcentage).
Exemple 2 : représenter l’angle correspondant à une pente de 10%.
La fonction qui à tout angle aigu α associe sa pente s’appelle la tangente de l’angle α.
Dans un triangle rectangle ABC rectangle en B, tan(α) = 
tan(α) =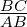 
Exemple :
tan(α) = 
La calculatrice permet de déterminer α grâce à la fonction "arctan" ou "tan-1" : α ≃ 36,9∘.
C’ est un point quelconque de la demi-droite [AC)
On s’intéresse maintenant au rapport 
Mesurer et calculer 
et 
. Que peut-on conjecturer?
Il semble que cela soit toujours le même : autrement dit, ce rapport ne dépend que de l’angle α.
Démonstration :
(BC)∕∕(B′C′) (car perpendiculaires à une même droite).
D’après le théorème de Thalès : 
= 
égalité des produits en croix : AB × AC′ = AC × AB′
On divise chaque membre de l’égalité par AC :
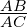× AC′ = AB′
On divise chaque membre de l’égalité par AC’ :
On obtient l’égalité : 
= 
Le rapport 
ne dépend donc que de l’angle α.
Ce rapport est appelé "cosinus" de l’angle α. cos(α) = 
Dans un triangle rectangle ABC rectangle en B, cos(α) = 
On pourrait faire la même démonstration pour le rapport 
. On appelle ce dernier rapport le "sinus" de
l’angle α.
sin(α) =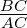 
Dans un triangle rectangle ABC rectangle en B,sin(α) =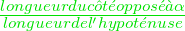 
.
Pour mémoriser les trois rapports trigonométriques :
cos(angle) =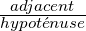 
CAH
sin(angle) = 
SOH
tan(angle) =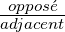 
TOA
à l’oral : 9 à 12 p 208
à l’écrit (écrire les rapports trigonométriques) : 23 à 27 p 209
Le cosinus d’un angle est le sinus de l’angle complémentaire
α et β sont complémentaires : α + β = 90∘
cos(α) = 
sin(β) = 
Le cosinus et le sinus d’un angle aigu sont des nombres strictement compris entre 0 et 1
car l’hypoténuse (au dénominateur) est toujours plus grand que le côté adjacent ou le côté opposé (au numérateur).