La balance inertielle
Par GEP Versailles le 01 avril 2010, 11:27 - Lien permanent
Comment déterminer la masse d’un objet en impesanteur ?
Activité pour la classe de terminale S
Astronautes près de la station spatiale internationale (source : Nasa)
Dans la station spatiale internationale, les astronautes ne ressentent plus l’effet de la pesanteur, ils « flottent » sans être attirés vers le sol de la station. Dans ces conditions, comment leur serait-il possible de peser un objet, ou de se peser eux-mêmes ? Dans l’espace, les balances traditionnelles semblent dépourvues d’intérêt.
Pourtant, la masse d’un objet pourrait bien être déterminée en mesurant un autre paramètre que son poids. Rappelons que la masse est directement liée à l’inertie : plus la masse d’un objet est grande, plus il est difficile de le mettre en mouvement, ou de modifier son mouvement.
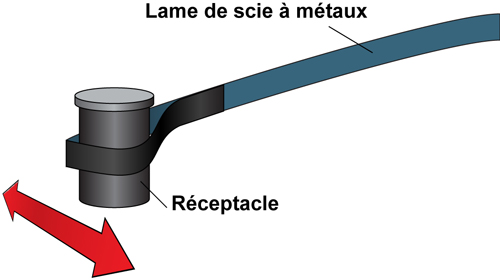
Nous allons étudier un dispositif très simple, constitué d’une lame de scie à métaux et d’une boite à pellicule photo. Cet appareil pourrait-il aider les astronautes à déterminer la masse d’un objet ?
Regarder attentivement la vidéo ci-après qui présente l’appareil, baptisé “balance inertielle” (”inertial balance”) par le site internet de la Nasa. Il est conseillé de visualiser la vidéo en mode plein écran et en haute définition.
Votre objectif consiste à déterminer la masse approximative d’une pièce d’un euro à l’aide de la balance inertielle.
Tout d’abord, voici le récapitulatif des mesures permettant de construire la droite d’étalonnage (il est possible, aussi, de télécharger ces données au format OpenOffice 3 ou au format Excel 2003) :
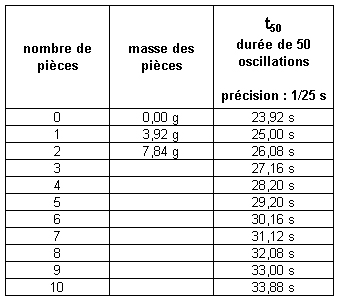
Compléter la colonne centrale du tableau, et tracer (sur ordinateur, ou sur papier millimétré) l’ensemble des points (m ; t50^2). Comme dans la vidéo, tracer la droite passant au plus proche des points, et déterminer son équation.
Ensuite, mesurer la durée de 50 oscillations de la balance lorsqu’elle est chargée avec cinq pièces d’un euro, de masse inconnue : visualiser la vidéo et utiliser les boutons pour compter les images. La durée séparant chaque image est, rappelons-le, de 1/25ème de seconde.
Déduire, à partir de la mesure de durée et de la droite d’étalonnage, une estimation de la masse totale des cinq pièces. Encadrer le résultat en tenant compte de l’incertitude de la mesure de la durée.
En déduire une estimation de la masse de l’une des cinq pièces d’un euro (les pièces sont considérées identiques), sous la forme d’un nouvel encadrement.
Rechercher sur internet, la masse réglementaire d’une pièce d’un euro. Votre résultat est-il en accord avec cette valeur ?
